[데이터베이스] 정규화 정리

1. 정규화(Normalization)

---

[ 정규화(Normalization)이란? ]

정규화(Normalization)의 기본 목표는 테이블 간에 중복된 데이터를 허용하지 않는다는 것이다. 중복된 데이터를 허용하지 않음으로써 무결성(Integrity)를 유지할 수 있으며, DB의 저장 용량 역시 줄일 수 있다.

 

[ 제1 정규화 ]

제1 정규화란 테이블의 컬럼이 원자값(Atomic Value, 하나의 값)을 갖도록 테이블을 분해하는 것이다.

 

규칙

1. 각 컬럼이 하나의 속성만을 가져야 한다.
2. 하나의 컬럼은 같은 종류나 타입(type)의 값을 가져야 한다.
3. 각 컬럼이 유일한(unique) 이름을 가져야 한다.
4. 칼럼의 순서가 상관없어야 한다.

위의 테이블에서 추신수와 박세리는 여러 개의 취미를 가지고 있기 때문에 제1 정규형을 만족하지 못하고 있다. 그렇기 때문에 이를 제1 정규화하여 분해할 수 있다. 제1 정규화를 진행한 테이블은 아래와 같다.

발생 할 수 있는 이상(Anomaly)

• 갱신이상
• 삭제이상

 

[ 제2 정규화 ]

제2 정규화란 제1 정규화를 진행한 테이블에 대해 완전 함수 종속을 만족하도록 테이블을 분해하는 것이다. 여기서 완전 함수 종속이라는 것은 기본키의 부분집합이 결정자가 되어선 안된다는 것을 의미한다.

규칙

1. 1정규형을 만족해야 한다.
2. 모든 컬럼이 부분적 종속(Partial Dependency)이 없어야 한다. -> 모든 칼럼이 완전 함수 종속을 만족해야 한다.

 

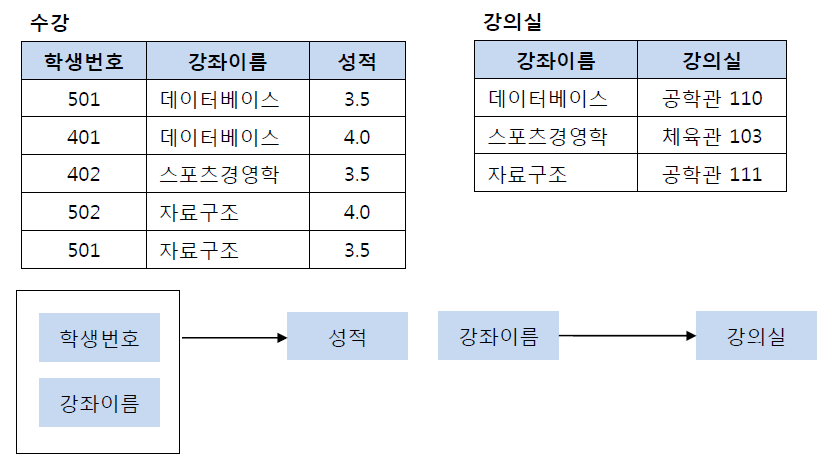
이 테이블에서 기본키는 (학생번호, 강좌이름)으로 복합키이다. 그리고 (학생번호, 강좌이름)인 기본키는 성적을 결정하고 있다. (학생번호, 강좌이름) --> (성적)
그런데 여기서 강의실이라는 컬럼은 기본키의 부분집합인 강좌이름에 의해 결정될 수 있다. (강좌이름) --> (강의실)
즉, 기본키(학생번호, 강좌이름)의 부분키인 강좌이름이 결정자이기 때문에 위의 테이블의 경우 다음과 같이 기존의 테이블에서 강의실을 분해하여 별도의 테이블로 관리하여 제2 정규형을 만족시킬 수 있다.

발생 할 수 있는 이상(Anomaly)

• 삽입이상
• 갱신이상
• 삭제이상

 

[ 제3 정규화 ]

제3 정규화란 제2 정규화를 진행한 테이블에 대해 이행적 종속을 없애도록 테이블을 분해하는 것이다. 여기서 이행적 종속이라는 것은 A -> B, B -> C가 성립할 때 A -> C가 성립되는 것을 의미한다.

규칙

1. 2 정규형을 만족해야 한다.
2. 기본키를 제외한 속성들 간의 이행 종속성 (Transitive Dependency)이 없어야 한다

 

 

기존의 테이블에서 학생 번호는 강좌 이름을 결정하고 있고, 강좌 이름은 수강료를 결정하고 있다. 그렇기 때문에 이를 (학생 번호, 강좌 이름) 테이블과 (강좌 이름, 수강료) 테이블로 분해해야 한다. 

이행적 종속을 제거하는 이유는 비교적 간단하다. 예를 들어 501번 학생이 수강하는 강좌가 스포츠경영학으로 변경되었다고 하자. 이행적 종속이 존재한다면 501번의 학생은 스포츠경영학이라는 수업을 20000원이라는 수강료로 듣게 된다. 물론 강좌 이름에 맞게 수강료를 다시 변경할 수 있지만, 이러한 번거로움을 해결하기 위해 제3 정규화를 하는 것이다.
즉, 학생 번호를 통해 강좌 이름을 참조하고, 강좌 이름으로 수강료를 참조하도록 테이블을 분해해야 하며 그 결과는 다음의 그림과 같다.

발생 할 수 있는 이상(Anomaly)

• 삽입이상
• 갱신이상
• 삭제이상

 

[ BCNF 정규화 ]

BCNF(Boyce-Codd Normal Form) 정규화란 제3 정규화를 진행한 테이블에 대해 모든 결정자가 후보키가 되도록 테이블을 분해하는 것이다. 예를 들어 다음과 같은 특강수강 테이블이 존재한다고 하자.

 

규칙

1. 3정규형을 만족해야 한다.
2. 모든 결정자가 후보키 집합에 속해야 한다.

 

 

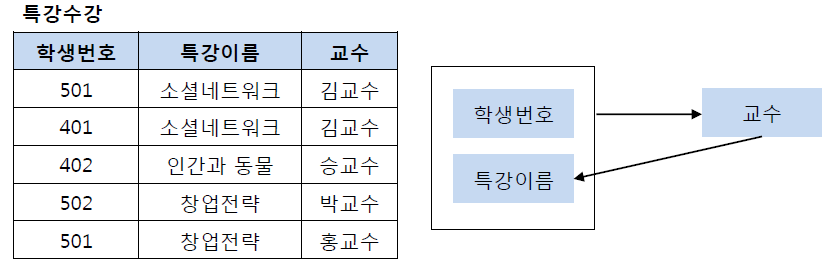
특강수강 테이블에서 기본키는 (학생번호, 특강이름)이다. 그리고 기본키 (학생번호, 특강이름)는 교수를 결정하고 있다. 또한 여기서 교수는 특강이름을 결정하고 있다.
그런데 문제는 교수가 특강이름을 결정하는 결정자이지만, 후보키가 아니라는 점이다. 그렇기 때문에 BCNF 정규화를 만족시키기 위해서 위의 테이블을 분해해야 하는데, 다음과 같이 특강신청 테이블과 특강교수 테이블로 분해할 수 있다.

 

발생 할 수 있는 이상(Anomaly)

• 삽입이상
• 갱신이상
• 삭제이상

 

[ 제4 정규화 ]

제4 정규형은 다음과 같은 규칙을 만족해야 한다.

 

규칙

1. BCNF를 만족해야 한다.
2. 다치 종속(Multi-valued Dependency)이 없어야 한다.

 

여기서 다치 종속이란 다음과 같은 조건들을 만족할 때를 뜻한다.

 

1. A->B 일 때 하나의 A값에 여러 개의 B값이 존재하면 다치 종속성을 가진다고 하고 A↠B라고 표시한다

2. 최소 3개의 칼럼이 존재한다.

3. R(A, B, C)가 있을 때 A와 B 사이에 다치 종속성이 있을 때 B와 C가 독립적이다.

 

[그림 1] 다치 종속

 

 

위와 같은 테이블을 보자. 101번 학생은 자바와 C++ 과목을 수강하고, 노래와 게임을 취미로 가진다. 

 

이렇게 되면 학생 번호 하나에 과목 여러 개와 취미 여러 개가 종속된다. 이런 경우 학생 번호를 토대로 값을 조회하면 아래와 같이 중복이 발생하게 된다.

 

[그림 2] 다치 종속성의 문제점

 

과목과 취미는 관계가 없는 독립적인 관계이다. 하지만 같은 테이블의 학생 번호라는 칼럼에 다치 종속되어버려 중복이 발생하는 문제가 생겼다.

 

 

4NF를 만족하기 위해서는 아래와 같이 분해하면 된다.

 

[그림 3] 4NF

 

위 2개의 테이블은 여전히 다치 종속성을 가지지만, 2개 이상의 칼럼이 하나의 칼럼에 다치 종속되지는 않기 때문에 제4 정규형을 만족한다.

 

 

[ 제5 정규화 ]

제5 정규형은 중복을 제거하기 위해 분해할 수 있을 만큼 전부 분해하는 것이다. 이러한 5NF는 Project Join Normal Form(PJNF)라고도 불린다. 이러한 제 5정규형은 다음과 같은 규칙을 만족해야 한다.

 

규칙

1. 4NF를 만족해야 한다.
2. 조인 종속(Join dependency)이 없어야 한다.
3. 조인 연산을 했을 때 손실이 없어야 한다.

 

조인 종속은 다치 종속의 좀 더 일반화된 형태이다. 만약 하나의 릴레이션을 여러 개의 릴레이션으로 무손실 분해했다가 다시 결합할 수 있다면 조인 종속이라고 한다.

 

[그림 4] 조인 종속

 

예를 들어 A라는 릴레이션을 B와 C로 분해했다가 다시 조인했을 때 그대로 A가 된다면, A는 조인 종속성이 있다고 한다.

 

 

 

출처
- https://mangkyu.tistory.com/110

[Database] 정규화(Normalization) 쉽게 이해하기

- https://code-lab1.tistory.com/270

[DB] 제 4정규형과 제 5정규형, 4NF와 5NF